Precision and recall (precision_recall)

Description

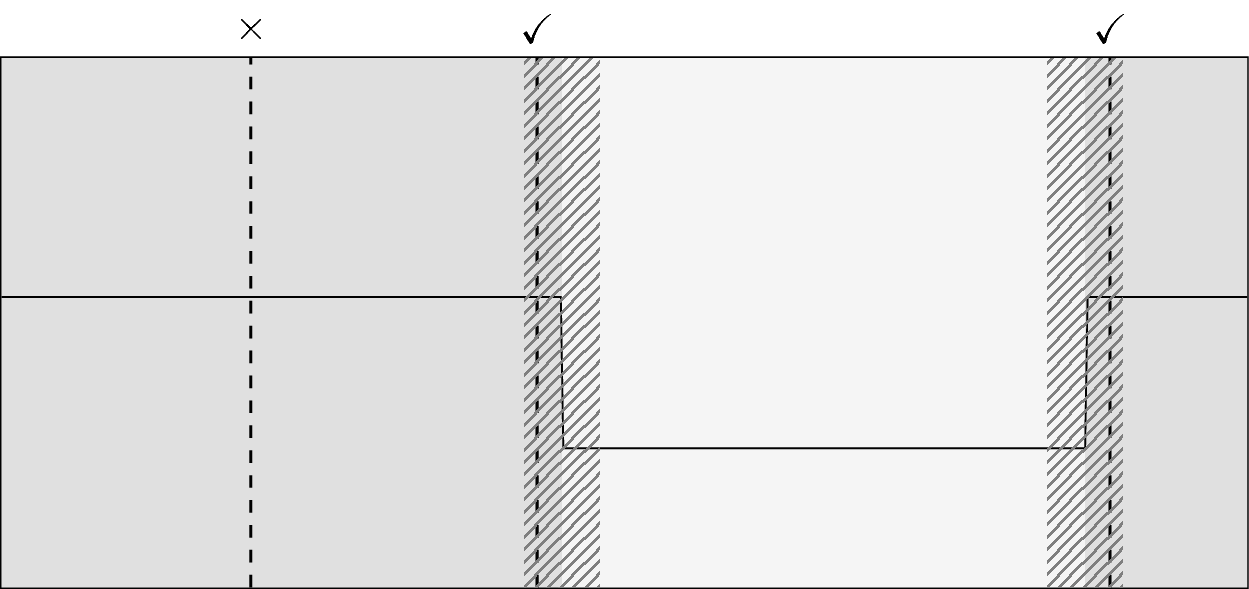
The precision and recall of an estimated segmentation is computed by the function precision_recall as follows. A true change point is declared "detected" (or positive) if there is at least one computed change point at less than "margin" points from it. Formally, assume a set of change point indexes \(t_1,t_2,\dots\) and their estimates \(\hat{t}_1, \hat{t}_2,\dots\) In the context of change point detection, precision and recall are defined as follows:

\[ \text{precision}:=|\text{TP}|/|\{\hat{t}_l\}_l| \quad \text{and}\quad\text{recall}:=|\text{TP}|/|\{t_k\}_k| \]

where, for a given margin \(M\), true positives \(\text{TP}\) are true change points for which there is an estimated one at less than \(M\) samples, i.e.

\[ \text{TP}:= \{t_k\,|\, \exists\, \hat{t}_l\,\, \text{s.t.}\, |\hat{t}_l - t_k|<M \}. \]

Schematic example: true segmentation in gray, estimated segmentation in dashed lines and margin in dashed areas. Here, precision is 2/3 and recall is 2/2.

Usage

Start with the usual imports and create two change point sets to compare.

from ruptures.metrics import precision_recall

bkps1, bkps2 = [100, 200, 500], [105, 115, 350, 400, 500]
p, r = precision_recall(bkps1, bkps2)
print((p, r))

The margin parameter \(M\) can be changed through the keyword margin (default is 10 samples).

p, r = precision_recall(bkps1, bkps2, margin=10)
print((p, r))
p, r = precision_recall(bkps1, bkps2, margin=20)
print((p, r))